《应用数学》教学大纲
一、课程概况
1、课程编码：
2、开课单位：理学院
3、适用专业：计算机应用技术
4、开课时间：第1、2、3、4学期
5、学 时：220学时
6、课程类型：专业必修课
7、考核方式：第1、2学期考试，第3、4学期考查
二、课程性质、任务与基本要求
1、课程的性质和任务
应用数学是本专业一门重要基础课，是进一步学习其他计算机专业课程的基础。它包括极限论、微分学、积分学、线性代数，概率论，图论等重要内容。它用极限方法研究函数的连续性、可微性、可积性等分析性质，并为研究以及应用创造了系统的、有效的理论和方法， 这些思想方法对于整个数学的思考、理解、探讨与应用都具有极其重要而深刻的意义。
通过本课程的教学，使学生掌握应用数学的基本内容和方法， 为后续课程打下良好的基础；为培养学生的严谨的数学思维能力和探索能力提供必要的训练；深入地理解数学分析的基本概念和基本理论，掌握典型的分析方法，使学生初步具备应用数学方法分析问题和解决问题的能力。
2、课程的教学基本要求
以简单的、基本的问题为导引，在教学过程中逐步引入极限概念，并随着课程的深入逐渐深化，引入连续性、可微性以及可积性中有关的基本概念并结合足够的练习使学生达到准确的理解，完成初等微积分的教学；在教学中要注意举例，包括正例与反例，同时要注意训练学生构造例子、分析例子的能力；在各个阶段的教学过程中，都要注意对应用数学基本理论的教学，比如实数的连续性问题，函数的连续性问题，函数列的收敛性问题等。 掌握基本的分析论证问题方法和技巧，训练学生的逻辑思维能力和表达能力；注意提炼总结典型的分析方法。通过数学分析的教学培养学生分析问题和解决问题的能力以及一定的计算能力，而且还要培养学生建立数学模型解决应用问题的能力；在教学中要注意由易到难，循序渐进。首先侧重概念和计算的练习，进而加强理论和方法的训练；在教学中要注意加强辅导，注意教学方法的灵活使用，设计必要的数学实验以辅助教学。
3、教学方法及教学形式的建议
教学方法: 概念和理论部分以课堂讲授为主，习题课师生共同参与。
教学形式: 多媒体教学手段。对重要的概念、定理、例子以及理解上较为困难的内容，要制作应用合适的幻灯片、动画辅助教学，以提高教学效果。但是，在通常的教学过程中，要严格控制对多媒体教学手段的使用，确保教学质量。有计划地开展数学实验教学活动，培养学生运用数学软件解决实际问题的能力。
4、课程教学要求的层次：
掌握：极限，微分，积分，行列式，矩阵的计算方法。
了解：定理的证明。
三、教学内容和教学要求
1、函数，极限与连续
【教学内容】函数及其图形，函数运算，初等数学模型，函数极限，无穷大量与无穷小量，极限运算，函数的连续性，生活中的极限问题，演示与实验一。
【教学目的与要求】理解函数的概念，了解函数的有界性，单调性，周期性与奇偶性，理解反函数与复合函数的概念，熟练掌握基本初等函数的性质与图形，能建立简单实际问题中的函数关系。了解极限ξ--√,ξ—N的定义，在整个学习过程中，逐步加深对极限思想的理解，掌握极限的四则运算法则，了解加逼准则和单调有限准则，会用两个重要极限求极限，了解无穷小，无穷大的概念，掌握无穷小的比较，会用等价无穷小的代换求极限，理解在一点连续的概念，会判断间断点的类型，了解初等函数的连续性，知道在闭区间上连续函数的性质。
2、导数与微分
【教学内容】导数概念，导数的基本公式与运算法则，特殊函数求导法及高阶导数，变化率问题实例，微分，演示与实验二。
【教学目的与要求】理解导数和微分的概念，了解导数的几何意义及函数可导性与连续性之间的关系。能用导数描述一些物理量的变化率。熟悉导数和微分的运算法则以及导数的基本形式。了解高阶导数的概念。能熟练的求初等函数的一阶和二阶导数，掌握隐函数和参数式函数的一阶和二阶导数。
3、导数应用
【教学内容】 函数的单调性，函数的极值，函数曲线的凹向与渐近线，简单最优化数学模型，演示与实验三。
【教学目的与要求】了解中值定理（罗尔中值定理，拉格朗日中值定理）的条件与结论，会熟练运用罗必塔法则求未定式的极限，理解函数的单调性，极值凹凸性及拐点的概念，会求函数的单调区间，极值，凹凸区间和拐点的概念，会求函数的单调区间，极值，凹凸区间和拐点，会描绘简单的图形，会解简单最大值，最小值的应用问题。
4、积分
【教学内容】定积分的概念与性质，微积分基本定理，基本积分法，无穷区间上的反常积分，演示与实验四。
【教学目的与要求】理解定积分的概念及性质，熟练掌握定积分的换元法，分步积分法。理解变上限定积分作为其上限函数，以及求导定理。熟练掌握和运用牛顿——莱布尼兹公式，掌握广义积分的计算方法。
5、积分的应用
【教学内容】定积分的微元法，平面图形的面积，空间立体的体积，其他应用实例，积分数学模型实例。
【教学目的与要求】理解微元法的基本思想。掌握直角坐标系F平面图形的面积的求法。掌握极坐标系F平面图形的面积的求法。掌握本行截面面积为已知的立体体积的求法。掌握旋转体体积的求法，会用微元法解一些几何和物理问题。
6、常微分方程
【教学内容】基本概念，一阶微分方程，二阶微分方程，演示与实验五，微分方程数学模型实例。
【教学目的与要求】了解微分方程的解、通解、特解和带有初始条件的的解的概念，熟练掌握变量可分离方程，其次方程和一阶线性微分方程的解法，熟悉下列特殊高阶微分方程的解法，y(n)=f(x).y’’=f(x•y’).了解常阶线性微公方程的解法结构，熟练掌握常导数二阶线性齐次方程的解法。
7、多元微积分简介
【教学内容】空间解析几何简介，多元函数的概念、极限和连续性，偏导数与全微分，复合函数和隐函数的微分法，多元函数的极值，二重积分，演示与实验六。
【教学目的与要求】理解空间直角坐标系，平面，曲面的基本概念，理解多元函数的概念知道二元函数的极限，连续性的概念，以及有界闭区域上连续函数的性质。熟悉偏导数，全微分等要领了解全微分存在的条件（必要及充分），熟练掌握复合函数的求导法，会求二阶偏导数及隐函数的偏导数，熟悉曲z一的切线与法平面，曲面的切平面与法线。并掌握它们的方程求法。理解多元函数极值的的概念，会求函数的极值，理解条件极值的概念。会使用拉格朗日乘数法求条件极值的方法解法最大值，最小值的应用问题，理解二重积分的概念，知道二重积分的性质，掌握二重积分的计算方法（直角坐标与极坐标）。能用二重积分表达和计算一些几何量。
8、无穷级数
【教学内容】常数项级数及其审敛法，幂级数，函数展开成幂级数，傅里叶级数，演示与实验七。
【教学目的与要求】理解常数项级数的概念，幂级数的概念，付里叶级数的概念。掌握常数项级数的判别法。幂级数的判别法。函数展开成幂级数的方法，付里叶级数的判别法。
9、数值计算初步
【教学内容】数值计算中的误差，函数插值法，方程
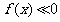的数值解法，数值积分，常微分方程的数值解法，演示与实验八。
【教学目的与要求】理解数值计算中的误差概念,会使用拉格朗日插位公式,会用二分法和牛顿切线法素数方程近似解,会用数值积分的矩形求积公式,抛物线法求积公式素进行积分近似计算,掌握常微分方程的数值解法。
10、行列式与矩阵
【教学内容】行列式，克拉默法则，矩阵及其运算，矩阵的初等变换与矩阵的秩，逆矩阵。
【教学目的与要求】理解n阶行列式的概念，能熟练的运用行列式的性质化简行列式，会用克莱姆法则解方程组，明确矩阵的概念，熟悉各种矩阵的运算，熟练初等行变换，理解矩阵和逆阵的概念，会求逆阵
11、线性方程组
【教学内容】线性方程组的消元法，线性方程组解的结构，线性代数的应用实例，演示与实验十。
【教学目的与要求】深刻理解n维向量的概念，了解向量的线性相关的熟悉向量组的秩，明确齐次线性方程组和非齐次方程组解的结构，会解齐次与非齐次线性方程组
12、随机事件与概率
【教学内容】随机事件及其概率，古典概型，事件的运算及概率的加法公式，条件概率、乘法公式与事件的独立性，全概公式与逆概公式，独立实验序列概型。
【教学目的与要求】了解随机事件，不可能事件，必然事件等概念，正确理解频率与概率，掌握古典概型及其计算方法，掌握并运用事件的运算条件概率，乘法公式及独立性，全概公式，逆概公式，独立试验序列等知识解决数学问题。
13、随机变量及其概率分布
【教学内容】随机变量，离散型随机变量及其分布规律，连续型随机变量及其分布，分布函数与随机变量函数的分布，计算机模拟与随机数的生成。
【教学目的与要求】了解随机变量的概念及其分类，掌握离散型和连续性随机变量几种常见的概率分布，初步掌握分布函数与随机变量函数的分布。
14、随机变量的数字特征
【教学内容】离散型随机变量的期望，连续型随机变量的期望，期望的简单性质及随机变量函数的期望，方差及其简单性质，随机优化数学模型实例，演示与实验十一。
【教学目的与要求】理解随机变量的数学期望的方差，掌握它们的简单性质，会用离散型随机变量的分布列和连续型随机变量的密度函数求数学期望，会用期望与方差的关系式求方差，并掌握几种常见分布的期望和方差。
15、集合论
【教学内容】集合，关系
【教学目的与要求】了解集合的有关概念，掌握集合的运算 ，理解关系的概念及性质。
16、数理逻辑
【教学内容】命题与联结词，公式的相等与蕴含，谓词与量词。
【教学目的与要求】掌握命题的概念，及五个常见的逻辑连接词及其真值表，会将命题符量化，掌握谓词与量词及更名规则。
17、图论
【教学内容】图的基本概念，无向图的连通性，有向图的连通性，无向图的矩阵表示，有向图的矩阵表示，欧拉图与哈密顿图，树。
【教学目的与要求】掌握图的基本概念，图的连通性及矩阵表示，会用欧拉图与哈密顿图解决有关的图论问题。掌握树的有关概念
四、教学课时安排与分配
序号 |
教学内容 |
课时安排 |
教学形式与场所 |
1 |
函数、极限与连续 |
22 |
应用多媒体课件讲授，多媒体教室 |
2 |
导数与微分 |
12 |
应用多媒体课件讲授，多媒体教室 |
3 |
导数应用 |
10 |
应用多媒体课件讲授，多媒体教室 |
4 |
积分 |
16 |
应用多媒体课件讲授，多媒体教室 |
5 |
积分的应用 |
8 |
应用多媒体课件讲授，多媒体教室 |
6 |
常微分方程 |
14 |
应用多媒体课件讲授，多媒体教室 |
7 |
多元微积分概念 |
18 |
应用多媒体课件讲授，多媒体教室 |
8 |
无穷方程 |
14 |
应用多媒体课件讲授，多媒体教室 |
9 |
数值计算初步 |
10 |
应用多媒体课件讲授，多媒体教室 |
10 |
行列式与矩阵 |
18 |
应用多媒体课件讲授，多媒体教室 |
11 |
线性方程组 |
14 |
应用多媒体课件讲授，多媒体教室 |
12 |
随机事件与概率 |
14 |
应用多媒体课件讲授，多媒体教室 |
13 |
随机变量及其概率分布 |
10 |
应用多媒体课件讲授，多媒体教室 |
14 |
随机变量的数字特征 |
8 |
应用多媒体课件讲授，多媒体教室 |
15 |
集合论 |
6 |
应用多媒体课件讲授，多媒体教室 |
16 |
数理逻辑 |
10 |
应用多媒体课件讲授，多媒体教室 |
17 |
图论 |
16 |
应用多媒体课件讲授，多媒体教室 |
五、教材与参考书目
使用教材：高等教育出版社编写的《计算机数学基础》（第三版）
教学参考书目：
1、《高等代数》张禾瑞 郝柄新 编高等教育出版社
2、《高等数学(二)第二分册概率统计》唐国兴 武汉大学出版社
3、《概率论与数理统计》浙江大学 高等教育出版社
4、《概率论与数理统计 》袁荫棠编 中国人民大学出版社
5、《离散数学》左孝凌 上海科学技术出版社
大纲制定者：李凌凌
教研室主任：
制定日期：2014.1.8
